Точка пересечения трех сфер - это место, где три сферы пересекаются друг с другом, образуя общую точку. Поиск такой точки может использоваться в различных областях, таких как геодезия, компьютерная графика и 3D-моделирование. В этом практическом руководстве мы рассмотрим шаги по нахождению точки пересечения трех сфер и предоставим вам несколько примеров, чтобы помочь вам лучше понять процесс.
Первый шаг в поиске точки пересечения трех сфер - это определение параметров каждой сферы. Эти параметры включают в себя координаты центра сферы и ее радиус. Центр сферы обычно задается в трехмерном пространстве с помощью трех координат (x, y, z), а радиус представляет собой расстояние от центра до поверхности сферы.
Второй шаг - это решение системы уравнений, где каждое уравнение представляет себе уравнение сферы. Для этого мы будем использовать метод Трилатерации, который основан на интерсекции трех сфер в трехмерном пространстве. Решение этой системы уравнений даст нам координаты точки пересечения трех сфер.
В завершение, мы приведем несколько примеров и пошаговых инструкций по нахождению точки пересечения трех сфер. Поможем вам разобраться в основах и научиться применять этот метод для конкретных задач.
Понятие и идея задачи
Идея задачи заключается в использовании геометрических вычислений и математических формул для определения координат точки пересечения сфер. Для решения данной задачи требуется знание основ геометрии, алгебры и вычислительной математики.
Для нахождения точки пересечения сфер можно использовать метод трех шаров, который основан на использовании системы уравнений, описывающих поверхности сфер. В решении задачи необходимо найти решение этой системы уравнений, которое будет соответствовать координатам точки пересечения.
В данной статье будет рассмотрен алгоритм решения задачи о нахождении точки пересечения трех сфер с использованием метода трех шаров. Также будет представлен пример практического применения данного алгоритма для определения положения объекта в пространстве.
| Определение | Метод трех шаров |
| Задача | Нахождение точки пересечения трех сфер |
| Идея | Использование геометрических вычислений и математических формул |
| Требования | Знание геометрии, алгебры и вычислительной математики |
| Алгоритм | Решение системы уравнений, описывающих поверхности сфер |
Принцип поиска точки пересечения сфер
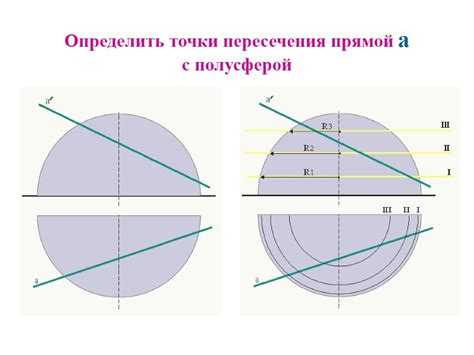
Для поиска точки пересечения трех сфер необходимо выполнить следующие шаги:
- Найти пересечение двух сфер
- Повторить шаг 1 для каждой пары сфер
- Получить пересечение всех трех найденных точек пересечения
Шаг 1: Нахождение пересечения двух сфер
Для нахождения пересечения двух сфер необходимо решить систему уравнений, в которой каждое уравнение описывает уравнение соответствующей сферы. Уравнение сферы имеет вид:
(x - a)^2 + (y - b)^2 + (z - c)^2 = r^2
где (x, y, z) - координаты точки на сфере, (a, b, c) - координаты центра сферы, r - радиус сферы.
Решив систему уравнений, можно получить две точки пересечения сферы.
Шаг 2: Повторение шага 1 для каждой пары сфер
Для нахождения точек пересечения трех сфер необходимо повторить шаг 1 для каждой пары сфер. Таким образом, будут найдены две точки пересечения для пары 1 и пары 2, две точки пересечения для пары 1 и пары 3, и две точки пересечения для пары 2 и пары 3.
Шаг 3: Получение пересечения всех трех найденных точек пересечения
После нахождения всех точек пересечения для каждой пары сфер, необходимо проверить их совместимость. Если все точки пересечения совпадают, то это и будет искомая точка пересечения трех сфер.
Если точки пересечения не совпадают, то это значит, что трех сфер не существует общей точки пересечения.
Как правило, точка пересечения сфер не единственна, поэтому возможно нахождение других точек пересечения, если они существуют. В таком случае, алгоритм может быть модифицирован для нахождения всех возможных точек пересечения трех сфер.
Необходимые математические инструменты

Для нахождения точки пересечения трех сфер вам понадобятся следующие математические инструменты:
- Геометрические понятия: векторы, точки, расстояния между точками, прямые;
- Уравнения окружностей: уравнение окружности в пространстве, радиус окружности, центр окружности;
- Решение систем уравнений: методы решения систем уравнений, такие как метод Гаусса или метод Крамера;
- Тригонометрия: теорема косинусов, теорема синусов.
Эти математические инструменты позволят вам анализировать геометрические конструкции и уравнения, связанные с трехмерным пространством и сферами. Они будут основой для решения задачи поиска точки пересечения трех сфер.
Шаги решения задачи на основе математических принципов

Для нахождения точки пересечения трех сфер требуется выполнить следующие шаги:
- Запишите данные о трех сферах. Для каждой сферы известны ее координаты центра (x, y, z) и радиус (r). Запишите эти данные в таблицу для удобства.
- Определите расстояние между центрами всех возможных попарных комбинаций сфер. Это можно сделать с помощью формулы для вычисления расстояния между двумя точками в трехмерном пространстве. Запишите полученные расстояния в таблицу.
- Проверьте, является ли задача выполнимой. Для этого нужно проверить, что расстояния между центрами сфер не превышают суммы радиусов этих сфер. Если это условие выполнено для всех трех попарных комбинаций, задача является выполнимой.
- Если задача является выполнимой, определите координаты точки пересечения сфер. Для этого можно воспользоваться системой уравнений, в которой каждое уравнение задает сферу. Решите эту систему уравнений для получения координат точки пересечения.
- Проверьте, что найденная точка действительно является пересечением трех сфер. Для этого проверьте, что расстояние от найденной точки до центра каждой сферы равно ее радиусу с заданной точностью.
При решении задачи необходимо учесть особенности работы с числами с плавающей запятой и округлениями. Также следует отметить, что в некоторых случаях трех сфер может не существовать пересечения, а искомой точке могут соответствовать несколько возможных позиций в пространстве. Для получения более точных результатов можно использовать численные методы.
| Сфера | Координаты центра (x, y, z) | Радиус (r) |
|---|---|---|
| Сфера 1 | (x1, y1, z1) | r1 |
| Сфера 2 | (x2, y2, z2) | r2 |
| Сфера 3 | (x3, y3, z3) | r3 |
Практические примеры решения задачи

Для нахождения точки пересечения трех сфер можно использовать алгоритм пересечения сфер методом триангуляции. Давайте рассмотрим несколько примеров решения такой задачи.
Пример 1:
Пусть у нас есть три сферы с заданными координатами центров и радиусами. Для простоты предположим, что центры всех трех сфер находятся на одной плоскости. Нам нужно найти точку пересечения этих сфер.
Шаги решения:
- Найдите все возможные пары сфер и найдите их точки пересечения.
- Используйте найденные точки пересечения для определения возможных треугольников.
- Выберите треугольник с наибольшей площадью.
- Найдите центр окружности, описанной вокруг выбранного треугольника.
- Полученная точка является точкой пересечения трех сфер.
Пример 2:
Предположим, у нас есть три сферы с заданными координатами центров и радиусами, и нам нужно найти точку пересечения этих сфер. В этом примере сферы могут находиться на разной высоте, то есть их центры могут иметь разные значения координат Z.
Шаги решения:
- Напишите функцию для нахождения точек пересечения двух сфер.
- Примените эту функцию к двум сферам и найдите точки пересечения.
- Найдите точки пересечения второй сферы с третьей сферой.
- Выберите точку пересечения, у которой значение координаты Z ближе всего к заданной высоте.
- Найденная точка будет точкой пересечения трех сфер.
Пример 3:
Предположим, у нас есть три сферы с заданными координатами центров и радиусами, и нам нужно найти точку пересечения этих сфер. В этом примере сферы могут находиться на разных плоскостях, то есть их центры могут иметь разные значения координат X, Y и Z.
Шаги решения:
- Найдите точки пересечения первой и второй сферы.
- Найдите точки пересечения первой и третьей сферы.
- Найдите точки пересечения второй и третьей сферы.
- Выберите точку пересечения, которая принадлежит пересечению всех трех пар сфер.
- Найденная точка будет точкой пересечения трех сфер.
Это только некоторые примеры алгоритмов решения задачи нахождения точки пересечения трех сфер. В каждом конкретном случае может потребоваться частичное или полное изменение алгоритма в зависимости от условий и требований задачи.